Di Fabio Mongile e Carlo Mauri
Abstract:
Il presente elaborato prende vita dall’incontro professionale di due autori, il dott. Carlo Mauri, commercialista brianzolo, appassionato di matematica ed esperto della Legge di Benford, curatore della rubrica “Cacciatori di numeri: Benford e altre Storie” e il dott. Fabio Mongile, investigatore, appassionato di criminologia e diritto penale ed esperto di antifrode assicurativa, curatore della rubrica “110 e frode”. L’obiettivo del presente elaborato è esporre i principi base della legge di Benford e la sua capacità di individuare su grandi sequenze di numeri eventuali frodi.
Indice:
1. La legge di Benford e le sue applicazioni scientifiche
2. La legge di Benford e le sue applicazioni in ambito di antifrode
3. La legge di Benford e le sue applicazioni in ambito di antifrode assicurativa
4. Conclusioni
1. La legge di Benford e le sue applicazioni scientifiche
Nel 1881 l’astronomo Simon Newcomb notò nel corso dei suoi studi che le tavole logaritmiche si presentavano maggiormente consumate nelle prime pagine e riscontrò questa stessa singolarità in ogni libro della biblioteca. In seguito, pubblicò un articolo sulla rivista American Journal of Mathematics, ma per circa cinquant’anni questa sua intuizione rimase lettera morta fino a quando, nel 1938, il fisico Frank Albert Benford coniò quella che conosciamo oggi come la legge di Benford, o anche legge della prima cifra.
Si tratta di un modello matematico-statistico che permette di prevedere aprioristicamente la frequenza con cui si distribuisce la prima cifra da sinistra nelle serie numeriche generate spontaneamente. Trattandosi di una rilevazione empirica non gode della definizione di teorema bensì di legge e ancora oggi è oggetto di indagine dei matematici.
Attraverso la legge di Benford è possibile rappresentare graficamente la curva di distribuzione delle ricorrenze della prima cifra significativa su grandi data set. La condizione necessaria perché sia applicabile è la casualità con la quale i numeri vengono generati e inoltre, ogni campione deve essere indipendente dagli altri e sufficientemente vario da abbracciare diversi ordini di grandezza (dalle decine alle migliaia). Non devono essere imposti limiti inferiori o superiori ai dati considerati e infine i numeri non devono essere di natura identificativa (come, ad esempio, i numeri di telefono o coordinate bancarie). Questo significa che non si può applicare la legge di Benford sui prelievi dagli ATM in quanto la cifra è vincolata al taglio delle banconote dello sportello automatico, sugli stipendi in quanto la cifra è predeterminata a monte o la statura di una popolazione, in quanto non abbraccia più ordini di grandezza. Qualunque altro genere di misurazione di origine casuale, indipendentemente dalla scala di riferimento, rispetterà questo principio statistico.
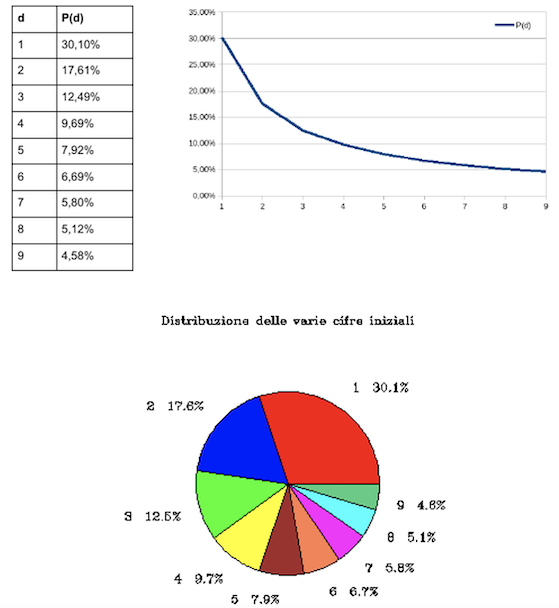
Immaginiamo di trovarci in un palazzo di nove piani con ascensore e un uguale numero di inquilini per piano. Ogni qualvolta che l’ascensore passerà il piano, anche senza fermarsi, il led corrispondente al numero del piano si illuminerà. Con che frequenza si illuminerà il led di ciascun numero?Il senso comune porterebbe a rispondere che la frequenza sarà equidistribuita per piano, ma in verità il numero 1 si illuminerà ogni volta che un inquilino prenderà l’ascensore mentre il numero 9 si illuminerà solo quando l’ascensore sarà chiamato dagli inquilini del nono piano. Viene da sé che la distribuzione della frequenza delle accensioni di ciascun led è inversamente proporzionale all’altezza del piano.
Benford ha declinato la sua legge nei più svariati campi di ricerca, raccogliendo numerose misurazioni e riscontrando che le grandi moli di dati seguivano pressoché analogamentela curva della distribuzione della prima cifra: la superficie dei fiumi, la popolazione, il peso atomico, il peso molecolare, i tassi di mortalità, solo per citarne alcune.
Recentemente la legge di Benford è stata utilizzata da numerosi studiosi al fine di verificare l’attendibilità dei propri dati. Tra questi, la geologa e vulcanologa Adelina GEYER, ricercatrice del CSIC (Consejo Superior de Investigationes Científicas), che in uno studio del 2012 ha utilizzato la legge di Benford per individuare errori, lacune o anomalie nella registrazione dei dati sui vulcani. Le prime due aree di verifica attengono all’estensione dei vulcani e alla loro età. La terza ha misurato la durata in giorni dell’eruzione. Il risultato ha portato a determinare che tutte e tre le misurazioni si conformano con la curva di Benford, ed era possibile identificare eventuali anomalie nei dati.
2. La legge di Benford e le sue applicazioni in ambito di antifrode
Il primo a intuire la possibilità di utilizzare la legge di Benford in ambito antifrode è stato nel 1992 Mark Nigrini, professore all’Università della West Virginia, che ha presentato la sua tesi di dottorato dal titolo “The detection of income evasion through an analysis of digital distributions” nella quale proponeva di confrontare “la curva di Benford” con le dichiarazioni dei redditi, individuando eventuali frodi fiscali. Immaginiamo ora di costituire una società fantasma (bad company) al fine di buttarvi dentro le passività di altre società “più virtuose”. A fine anno dovremmo presentare un bilancio ma, trattandosi di una società fittizia, gli importi delle fatture saranno ovviamente inventati. A questo punto, la distribuzione della prima cifra significativa presenterà delle gravi discordanze rispetto alla curva di distribuzione di Benford, nonostante gli importi di ciascuna fattura siano stati scelti casualmente. Difatti, come spiega anche Ted Hill nel suo “the difficulty of faking data”, l’elaborazione “casuale” di numeri da parte dell’uomo, non seguirà la naturale curva di distribuzione della legge di Benford, in quanto soggetta a processi mentali umani e, conseguentemente, di casuale avrà ben poco. Beninteso, la conformità con la curva di Benford non implica necessariamente la genuinità dei dati e la non conformità è semplicemente un indicatore sospetto che necessita di maggiore attenzione. Dopo la collaborazione con Nigrini le agenzie delle entrate di numerosi stati americani utilizzano ancora il suo software per monitorare le dichiarazioni dei redditi dei contribuenti.
La legge di Benford è entrata a pieno titolo tra gli strumenti in uso agli esperti di antifrode. L’ACFE (Association of Certified Fraud Examiners), da oltre dieci anni, ha inserito Benford tra i suoi programmi di studio e materia di esame, in quanto le sue potenzialità non sono circoscritte al solo ambito fiscale.
Walter R. Mebane Jr, professore di scienze politiche e di statistica dell’Università del Michigan, ha creato un software open source, “The Election Forensics Toolkit”. Il sistema si basa sull’assunto che la manipolazione per mano dell’uomo tende a lasciare delle tracce distintive nella conta dei voti. Manipolazioni individuabili confrontando la curva dei voti di ciascun distretto elettorale con la curva di distribuzione di Benford.
La manipolazione dei datiè argomento di estrema attualità in questi giorni, soprattutto in riferimento ai numeri della pandemia. Citiamo l’articolo di Gabriele Carelli sull’applicazione della legge di Benford ai morti di COVID in 32 paesi e in un arco temporale di 200 giorni. La ricerca ha portato a un risultato interessante: paesi come Regno Unito, Francia, Spagna, Germania e Italia hanno un RMSE (Root Mean Square Error, lo scarto quadratico medio) relativamente basso, ovvero il discostamento tra la curva ottenuta e la curva di Benford è minimo. Di contro, l’RMSE è decisamente più alto in paesi come l’Iran, il Perù, l’Arabia Saudita o la Russia. È stato poi effettuato un confronto con il democracy Index stilato nel 2019 dall’Economist Intelligence Unit e, come possiamo ben immaginare, salvo alcune eccezioni, all’aumentare del rank nel Democracy Index corrisponde uno scostamento più accentuato dalla distribuzione di Benford. In altre parole, con il diminuire dell’indice di democrazia aumentava la probabilità di alterazione dei dati.
In ambito forense la professoressa Jennifer Golbeck, docente di studi della comunicazione presso l’università del Maryland, ha effettuato uno studio su migliaia di profili social, selezionati casualmente. Ciascun profilo aveva un certo numero di followers e ciascun follower aveva a sua volta un numero X di followers. Analizzando la cifra X di ciascun profilo ha potuto constatare che tutti aderivano perfettamente alla curva di Benford. Una serie di account, al contrario, non rispettavano affatto questa distribuzione e, da un esame più approfondito di questi profili, è emerso che si trattava di bot russi. La professoressa Golbeck conclude che “l’applicabilità della legge di Benford ai social media è un nuovo strumento per analizzare il comportamento degli utenti e capire quando e perché possono verificarsi deviazioni rilevando così quando siano in atto forze anomale”.
I social oggi non sono però infestati solo di profili falsi, ma anche di immagini ritoccate. Spesso non si tratta solo di innocenti ritocchi di carattere estetico, ma di vere e proprie manipolazioni della realtà (deepfake). Questo fenomeno rischia di assumere delle connotazioni estremamente pericolose. Immaginiamo le dichiarazioni false e incredibilmente sopra le righe attribuite ad alcuni politici o personaggi famosi, il cyberbullismo o il revenge porn. Recentemente il garante delle privacy ha aperto un’istruttoria nei confronti di Telegram, per via del software deepnude, che permetteva di “spogliare” le donne, spesso minorenni. Oggi più che mai, a causa dell’intelligenza artificiale, è estremamente difficile distinguere un’immagine originale da un fake.
Gli effetti di un simile fenomeno rischiano di essere disastrosi, in quanto si arriva a sovvertire completamente il valore di una fotografia o di un video, non solo in ambito probatorio, ma anche in termini di media e informazione. Verità e bugia si fondono e si confondono. Non si sa più a cosa credere ed è in questo clima che le fake news dilagano e prendono vita. Dopo aver creduto per anni alle bugie in rete, il prossimo “passo” è quello di non credere più a ciò che è vero.
L’informatico, Hany Farid spiega che un’immagine in jpeg è composta da milioni di valori numerici generati casualmente e come tali rispetteranno la curva di Benford. Nel momento in cui l’immagine viene modificata, verrà salvata nuovamente. Ogni modifica comporterà un salvataggio e ogni salvataggio porterà a un appiattimento della curva dei valori dell’immagine, discostandosi dalla curva ideale di Benford. Questo permette ai tecnici forensi di individuare eventuali manipolazioni delle immagini.
3. La legge di Benford e le sue applicazioni in ambito di antifrode assicurativa
In tema di indagini in ambito assicurativo il lavoro di Hany Farid sull’analisi forense delle immagini digitali è sicuramente uno strumento prezioso. Laddove le perizie vengono eseguite su immagini digitali, le frodi possono essere operate tramite il fotoritocco. La circostanza più frequente e di facile attuazione è, come al solito, il danno automobilistico, ma pensiamo ai danni ai fabbricati derivanti da eventi atmosferici, i segni di effrazione a seguito di un furto e così via. Ogniqualvolta un danno viene documentato per immagini, questo potrebbe essere oggetto di sovrastima.
Tuttavia, come abbiamo detto, la legge di Benford si applica a grandi moli di dati generati casualmente e, pertanto, quale miglior applicazione se non i database delle imprese di assicurazione? Nel 2002 negli USA è stata proposta una ricerca dal titolo “Using Benford’s Law to Detect Fraud in the Insurance Industry”, la quale verteva su quattro grandi compagnie assicurative americane su sinistri aperti su polizze sanitarie in un periodo di 10 mesi, tra il 01.01.2001 e il 31.10.2001. I nomi delle quattro compagnie assicurative non sono stati menzionati per ragioni di privacy. Stando a quanto si legge nella ricerca, in seguito allo studio, le compagnie hanno continuato ad avvalersi della legge di Benford per indagare su eventuali frodi. L’analisi ha determinato che la distribuzione della prima cifra dell’ammontare delle richieste di risarcimento danni era in linea con la curva di Benford. È stata effettuata la stessa verifica prendendo in esame le prime due cifre, ma non della richiesta risarcitoria, bensì di ciascuna parcella sanitaria prodotta. Esaminando dunque i numeri da 10 a 99 è emerso che, seppure l’andamento seguisse per sommi capi la distribuzione attesa, la maggiore frequenza delle prime due cifre ricorrenti era sempre 10, 15, 20, 25, 30, 35…
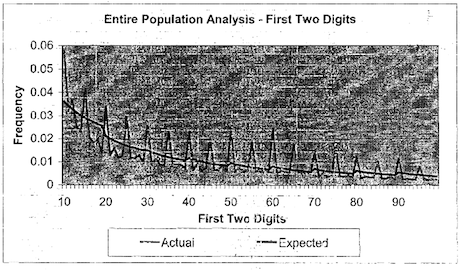
Questo ha permesso di determinare che le strutture sanitarie e il personale medico avessero arrotondato le parcelle al fine di massimizzare i profitti. Chiaramente non possiamo parlare in questo specifico caso di frode assicurativa, ma lo studio ha permesso di implementare una revisione periodica per rilevare se ci fossero delle tendenze anomale nei dati ricevuti dai vari fornitori.
Allo stato attuale, la letteratura in materia assicurativa è molto scarsa, ma siamo certi che un’analisi costante dei sinistri, anche in altri rami, quali ad esempio il settore auto che da sempre è quello più vessato dalle frodi assicurative, permetterebbe di tenere monitorato l’andamento della curva e di intervenire tempestivamente ove si rendesse necessaria un’indagine.
4. Conclusioni
Come abbiamo potuto comprendere, la legge di Benford è applicabile in qualunque campo ricorrano grandi moli di numeri casuali come le scienze naturali, le scienze umane o le scienze forensi. Da quasi trent’anni è diventato uno strumento nelle mani degli esperti dell’antifrode, ma le sue potenzialità latenti sono ancora inesplorate.
In ambito assicurativo, possiamo immaginare di effettuare delle analisi mirate, di modo da concentrare le successive indagini sui grandi produttori di cifre (sinistri) come ad esempio carrozzerie, strutture sanitarie pubbliche o private, periti, agenzie assicurative. Altresì, la curva di Benford può essere utilizzata su base territoriale al fine di individuare i luoghi “più caldi” dove abbondano anomalie nella curva di distribuzione della prima cifra.
Ovviamente, come tutti gli strumenti di indagine ha dei limiti: la non corrispondenza con la curva non è elemento sufficiente per individuare una o più frodi, ma è decisamente un ottimo indicatore di allarme che permetterebbe agli analisti di orientare le indagini restringendo il campo di ricerca. Di contro, la corrispondenza con la curva non dimostra, in termini assoluti, l’assenza di frodi. Difatti, la forza di questo strumento è oggi nella sua scarsa notorietà negli ambienti criminali, e non solo. Già Nigrini nei primi anni Novanta aveva capito come la mente umana non fosse in grado, spontaneamente, di generare una sequenza di numeri che, se aggregata, rispetti la distribuzione di Benford, ma il truffatore che dovesse conoscere questa legge sarà senz’altro in grado di prestarvi attenzione affinché i numeri inventati rispettino la legge e non si discostino dalla curva attesa di modo da non destare sospetti.
Generare sequenze di dati che riescano a soddisfare contemporaneamente gli intenti fraudolenti e il rispetto della distribuzione dalla Legge di Benford è estremamente complesso, seppure costituisca un rischio reale che vanificherebbe l’intero impianto antifrode. Alex Ely Kossovsky, della New York University, ha trovato una soluzione sviluppando un procedimento (la cui proprietà intellettuale è coperta da brevetto negli U.S.A.).
Tale procedimento si chiama “Modello di Sviluppato Digitale” e si propone come un metodo di analisi più evoluto rispetto alla legge di Benford ma che prende le mosse dalla stessa. La metodologia segue un determinato algoritmo che si basa sulla seguente constatazione empiricamente verificabile: se una serie di dati, conforme alla legge di Benford, viene ordinata in maniera crescente e i dati vengono raggruppati in sottoinsiemi secondo il loro ordine decimale: unità, decine, centinaia, migliaia, decine di migliaia etc. e se in ciascun sottoinsieme si applica il calcolo della legge di Benford sulla prima cifra, allora si ottiene che per gli insiemi più a sinistra della serie (le unità e le decine) le cifre tendono ad essere più equidistribuite tra loro (la curva sarà più piatta); per gli insiemi centrali (centinaia, migliaia etc..) la tendenza a conformarsi a Benford aumenta man mano che si arriva al “centro“ dei sottosistemi; per i sottoinsiemi più a destra (centinaia di migliaia, milioni…) si arriva ad avere una forte diseguaglianza distributiva delle prime cifre a favore dell’1 e del 2.
Questa logica distributiva segue quindi un preciso schema misurabile. Insomma, se una serie numerica, pur essendo nel complesso conforme a Benford, non è conforme allo “Schema di Sviluppo Digitale di Kossovsky”, allora tale serie ha elevate probabilità di essere stata oggetto di una sofisticata duplice manipolazione.


